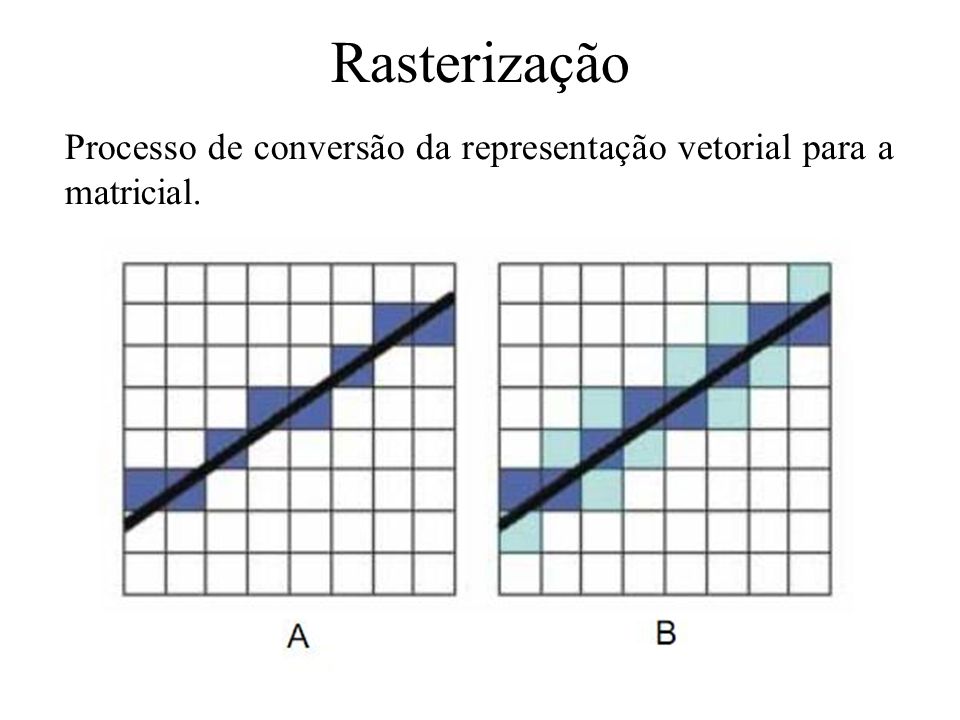
O objetivo deste segundo trabalho é a
construção de um pipeline gráfico, para a transformação de pontos do espaço do
objeto para o espaço de tela.
Com a utilização do que foi feito no
trabalho anterior, que foi a implementação da rasterização de pontos para o
espaço de tela, iremos agora implementar todas as transformações incorporadas
ao pipeline.
O pipeline são transformações que
devemos fazer um de espaço para outro até chegarmos na tela, como está na
figura abaixo:
Matriz Model - Espaço do objeto para o Espaço do universo
Foi utilizada a matriz Model para transformar os vértices do espaço do
objeto para o espaço do universo, onde podemos realizar transformações
como rotação, translação, escala e shear, é o passo inicial do pipeline gráfico.
Matriz View - Espaço do universo para o Espaço da câmera
O próximo passo é levar o objeto agora no espaço do universo para o espaço da câmera, onde vamos usar a matriz view, para isso devemos definir de onde serão visualizados os objetos, ou seja, quais as coordenadas da câmera e para onde ela está olhando. Na verdade a câmera estará sempre localizada na origem olhando para o sentido negativo do eixo z. O que muda são as coordenadas dos vértices dos objetos, que passam por uma mudança de sistema de coordenadas. Quando este processo ocorre, dizemos levar os vértices do espaço do universo paro o “espaço da câmera”.
O nosso vetor
posição, referencia a posição da câmera no espaço do universo. A nossa direção
na câmera, diz respeito a direção que a câmera está apontando na tela. O nosso
vetor up, nos referencia o vetor correspondente a parte superior da cena, por
exemplo {0,1,0} nos diz que a parte superior da nossa cena está presente no
eixo y.
Dessa forma, considerando todos
estes fatores, podemos agora construir a nossa Matriz View, que se
apresenta da seguinte maneira:
Espaço da câmera para o Espaço de Recorte
Agora os vértices
serão multiplicados por uma matriz especial chamada projection. Essa matriz leva os vértices do espaço
da câmera para o “espaço de recorte”. A multiplicação por essa matriz irá
definir o tipo de projeção, podendo ser ortogonal ou perspectiva. A projeção
perspectiva permite a sensação de profundidade dos objetos na tela, o mesmo não
ocorre com a projeção ortogonal. Outro detalhe é que a projeção ortogonal
preserva o paralelismo das retas, já a projeção perspectiva não.
Os objetos que estão mais perto do nosso view plane tem de se apresentar
maiores e objetos que estão mais longe com um tamanho menor.
De acordo com as características que nos pudemos perceber ate o momento e com o
auxilio da imagem acima, iremos agora explicar os passos necessários para a
criação da nossa matriz de projeção perspectiva.
O nosso ponto p, como podemos ver na
figura 8, após a aplicação de um distanciamento, terá, de acordo com as
características da projeção perspectiva um novo valor, ao qual nomeamos de p'.
Sabendo que d é a nossa distancia focal
da câmera e que y é o valor do objeto antes de passar pela projeção em
questão e y' é o valor do objeto depois de passar pela mesma, podemos
agora encontrar os valores de x', y' e z', valores estes
que representam o objeto após passar pelo processo de transformação. Para
obtenção desses valores, nós podemos usar a nosso favor a semelhança de
triângulos, pois, o nosso triângulo maior, que tem os lados cp, z+d e
y é proporcional ao nosso triangulo menor cp', d e y'. Após
aplicado a matriz projection, ela nos dará o seguinte efeito:
Podemos
representar dessa maneira:
Espaço de recorte para o Espaço canônico
Neste ponto, iremos
levar todos os vértices agora presentes no espaço de recorte, pra o espaço
canônico. Para isso, devemos dividir todas as coordenadas dos nossos pontos
pela coordenada homogênea, para que possamos gerar uma noção de profundidade na
cena.
Para traduzir todos
os nossos pontos para o espaço canônico, nós teremos que dividir todas as
nossas coordenadas x, y, z pela coordenada homogênea w e além disso ignorar tal
coordenada
Podemos
representar dessa maneira:
Espaço Canônico para o Espaço da tela
Sendo uma das últimas etapas do pipeline gráfico, essa transformação mapeia os vértices do espaço canônico para o espaço da tela, através de duas escalas e uma translação, levando todos os vértices para a parte positiva do sistema
A escala é feita a
partir de seus coeficientes escalares com os valores de largura (width) e
altura (height). A escala é aplicada com o intuito de escalar o nosso objeto a
um tamanho considerável na tela.
Depois de feito a
escala do nosso objeto, para leva-lo ao espaço de tela precisamos percorrer um
ultimo passo, que é a translação. Pois os pontos que se apresentam com valor
menor do que 0 ainda não foram tratados e se não forem, ficarão fora do nosso
espaço de tela quando aplicarmos o processo de rasterização. Dito isto,
aplicaremos agora o nosso objeto a nossa matriz de translação.
Implementação
Com base em tudo que foi apresentado até agora a implementação consiste no desenvolvimento da leitura de arquivos .obj para leitura de vértices e faces, o processamento de todos os pontos por todo pipeline gráfico, animação do objeto e impressão do modelo na tela. Após tudo que foi apresentado e com a implementação do que foi citado, podemos chegar ao seguinte resultado:
Material disponibilizado pelo professor Christian Pagot